Jeff Miller has done a couple of nice posts on “A Simulation of Angel Investing” here and here. I think it’s terrific that Jeff actually asked the question and tried to answer it with simulation. However, his answer of 20 is way too low because of two key oversimplifications. Using a more sophisticated methodology, I’ll show that a better answer is 100 to 150.
You may recall that Saving the World with Startups explained the “why” of RSCM. Our goal is to increase the number of technology startups. In some sense, this post describes the “how”. Well, at least part of it. One of the biggest barriers to getting a company off the ground is finding working capital. Ergo, we need to figure out how to facilitate investments in startups. More precisely, we need to promote seed-stage investments because those are what help founders initially launch their companies.
The ideal solution would be an investment vehicle that can turn huge chunks of money into digestible seed-stage bites with a return that induces plenty of investors to participate. But here are some slightly scary statistics. 50% of all seed-stage startups fail and returns come disproportionately from the top 10%. As all you poker players in the audience will note, you’re making big bets with high variance. The natural question is, “How many bets should you place?”
To answer this question, I’ve built several generations of seed-stage investing simulations for RSCM. My models are rather complicated because we wanted to evaluate a bunch of secondary questions such as whether it’s better to do follow on investments, what happens if the balance between seed and Series A valuations changes, and what happens in cases where a startup does poorly initially but then takes off. Therefore, I actually had to model the startup lifecycle round by round and the mechanics became very complex. (If you’re not a quant, you can stop reading now. Things are going to get real geeky real fast).
However, a simplified single-round version of my model will illustrate the missing pieces of Jeff’s model. The first is what diversification means. He focuses on the risk of total loss and the chances of not getting at least one “hit”. In my opinion, the question you really want to ask is what the probability is that you’ll under-perform the market by more than a given amount. For example, what’s the probability that you’ll under-perform by more than 25%? The logic here is that you invest in an asset class because of the overall return of that asset class, so you want to know the chances that you’ll realize returns in that ballpark.
The second key oversimplification is that Jeff uses a discrete probability distribution of returns. If you’ve read Taleb’s The Black Swan, you know this is a mistake because at least some seed-stage outcomes probably follow a Pareto distribution. The key characteristic of this distribution is that regions of extreme outcomes are self similar. So not only do the top 10% of companies represent a disproportionate share of the returns, the top 10% of the top 10% represent a disproportionate share of those returns. And so on. And so on. 20 investments may be enough to get you a fair share of the top 10%, but not enough to get you a fair share of the top 1%.
So here’s my simplified model, which roughly follows Jeff’s qualitative taxonomy:
- 50% failures: the company utterly fails. The investor gets 0 money returned.
- 20% break even: the company achieves some limited success and the money returned follows a lognormal distribution with a minimum of 0, a, mean of 1, and a standard deviation of 1. So an average outcome is 1.0x and 1 standard deviation above is 2.0x.
- 20% decent: the company achieves substantial success and the money returned follows a lognormal distribution with a minimum of 2, a mean of 4, and a standard deviation of 4. So the minimum outcome is 2x, the mean outcome is 4x, and 1 standard deviation above is 8x.
- 10% homeruns: the company achieves massive success and the money returned follows a Pareto distribution with a location of 10 and an index of 1.5. So the minimum outcome is 10x and the mean outcome is 30x.
Now, we can compute the expected value of an investment as .50*0 + .2*1 + .2*4 + .1 *30 = 4.0. The data I’ve seen puts the average hold time for successful angel investments at 6 years, so this would imply an IRR of about 26%. This is in line with the available research on angel returns (RSCM has a summary of this research here).
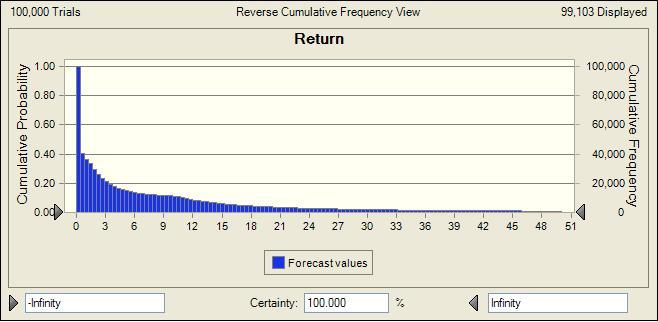
I ran a simulation with these parameters using Oracle’s Crystal Ball, producing an overall return distribution for a run of 100K trials. Here’s the excess distribution plot (the probability that the money returned will exceed a given multiple), truncated at 50x for some semblance of readability:
The return across the entire simulation was 4.05x (very close to the analytically expected return of 4.0x). The maximum return was 8,361x (think Andy Bechtolsheim‘s $100K investment in Google which was eventually worth about $1B). The top 10% accounted for 77% of the total return. The top 1% accounted for 35%. The top .1% accounted for 17%. We can already see that a portfolio of 20 will be insufficient.
The source file is AngelSimulation. Most of you probably don’t have Crystal Ball so this will look like a pretty useless Excel file to you. However, I set up the run to output just the AngelSimulationData in an Excel file. Anyone can analyze this with standard charting tools or import the data for use by his own code.
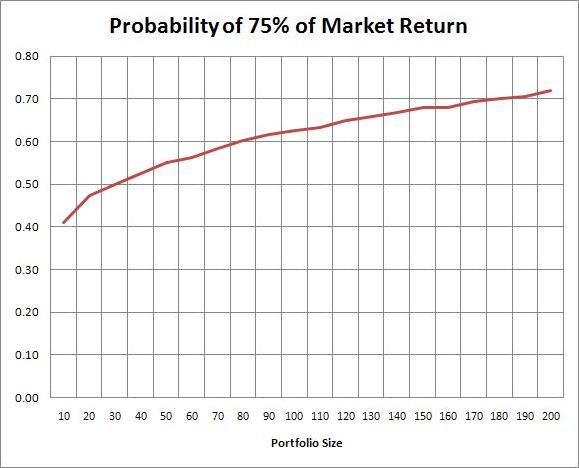
I’ve also got another AngelSimulationPortfolios with a macro that generates 10K random portfolios of a given size from the trial data. I’ve run it for portfolio sizes from 10 to 200 in intervals of 10. After sorting the portfolio returns at the specified size, the macro calculates the probability of hitting 75% of the market return by seeing what percentage of the portfolio returns are greater than 3.0. Here’s a chart of those probabilities:
[Edited 5/14 in response to suggestion from AN]. As you can see, 20 investments isn’t nearly enough if you’re a fund investing other people’s money. Worse than a coin flip that you’ll hit 75% of the market return. In fact, in my simulated portfolio data, there’s about a 7% chance that you’ll lose money with a portfolio of 20 investments. Personally, I’d say you want a fund to be in the 100 to 150 investment range. But it’s different for individual investors putting in their own money. I’d say you want to hit at least a 50% chance of realizing 75% of the market return, which would be 30 investments. Now, if you think you think you have some forecasting skill and less than 50% of your seed investments will fail and/or more than 10% will be homeruns, 20 may be plenty.
Of course, if you accept the thesis that 100-150 is the right range for a fully diversified fund-like portfolio, you may now be asking yourself how making that many seed-stage investments is logistically possible. The challenge is actually worse than that. Due to vintage risk, you probably want to make 100-150 investments per year or at least every few years. But that’s a story for another day…

Nice simulation.I agree that if you make the payoff distribution more lottery-like, you're going to want to buy more tickets.
Thanks, Jeff. Yep, the question is how lottery-like angel investing is.We have some data. We know Bechtolsheim got about 10,000x on his Google investment. It looks like Hoffman and Thiel could get about 5,000x on Facebook. If you look at the AIPP data set assembled by Wiltbank (http://sites.kauffman.org/aipp/request_download…), we have data on 466 exited angel investments. By multiple, the top 10% accounted for 67% of the liquidity. The top 5% accounted for 52%. The top 1% accounted for 12% (though the sample size is really too small to say anything about the top 1%).So the evidence looks like the skew is pretty high.
Assuming the same investment market, if I’m going to do between 50-80 investments, what are my chances of going broke? What if I did this for three years in a row?
What are my chances of beating 10% IRR as a function of number of investments? Chances of beating 20% IRR? 30% IRR?
Instead of this VAR-style analysis, how about something more like the Kelly Criterion?
The Kelly Criterion applies to Bernoulli trials. I looked at the Kelly Criterion math not too long ago and it seemed like it would be inherently problematic to apply to anything with a Pareto distribution. If you’ve got ideas along these lines, I’d love to hear them.
Yes, you can’t apply the Kelly Criterion directly. I’ll send you a spreadsheet when I get a chance.
I can send you the spreadsheet with all the portfolios if you want to answer these questions. My quick answer is that of 10K portfolios with 80 investments, only 7 lost money in my simulation. The worst returned 79 cents on the dollar. At 50 investments, 58 portfolios out of 10K lost money and the worst was 39 cents on the dollar.
The IRR question is trickier because my spreadsheet calculates payoff multiple. A conservative hold time for a successful investment is five years, so a 10% IRR would be a 1.6x payoff multiple.
For 80 investment in a portfolio, the chance of less than a 1.6x payoff multiple was about 2%. For 50, it was about 6%.
Please note that the simulation assumes independent identically distributed trials. In the real world, there will be correlations for vintage years, sectors, and geographies. Not to mention potential selection bias.